Introduction to Geometry

Mathematics fosters procedural thinking – Antony Kagirison

Point, Endpoints, and Angles

• Any specific location in space can be indicated by a point.
• The shortest distance between two points (i.e arbitrary Point A and Point B) is a straight line. In this line, Points A and B are called endpoints, and the line between these endpoints is called a line segment. Therefore, endpoints mark the points of termination of a line segment. Multiple endpoints on a single line allow one to divide the line into multiple segments. Line segments are critical in geometry.

• An infinite line has a specific starting point but does not have a termination point. This infinite line is called a ray if its direction of travel is indicated.
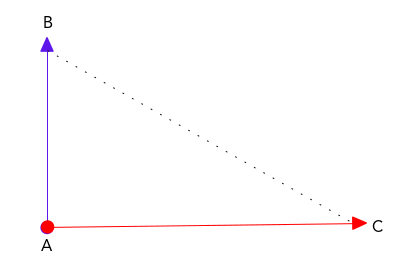
• If the ray starts at endpoint A and passes through Point B, then the line is denoted as Ray AB ( and as shown below, the arrowhead indicates the direction of the line). Therefore, Ray AB is not the same as Ray BA. The line segment in this ray is denoted as Segment AB.

• If there is a point C between A and B, then the line has three points that divide it into two line segments. If the length of line AB is known, and the length of segment AC is known, then the distance of CB can be calculated as:

CB = AB – AC

• The above formula is based on the segment addition postulate, which states that if a point (C) lies between two endpoints (A and B), then the distance between either endpoint to the point can be calculated as follows:

Distance between endpoints A and B (AB) = Distance between Endoint A and Point C (AC) + Distance between Point C and Endpoint (CB)

• If two rays intersect at a common endpoint, the point of intersection is called a vertex. Normally, this vertex is the endpoint where the two rays originate and move outwards in different directions as is indicated in the following diagram:

• If the two rays go in the same direction, then the angle between them at their vertex is 0 degrees, denoted as 0°; but if the rays go in opposite directions, then the angle at the vertex is 180°.

Angles

• The protractor is the device used to measure angles. It is shown below.

• The two main special types of angles are 90° which is called a right angle, and 180° which is called a straight angle.

• There are two special angle pairs: complementary angles which add up to 90°, and supplementary angles which add up to 180°.
• If Ray AB and Ray AC originate from vertex A, then the angle between ray AB and ray AC is written as ∠BAC or ∠CAB with A being in the middle to show that the center of the protractor is placed on vertex A. Likewise, it can be written simply as BAC or CAB. For geometers, these angles are written using one notation as ∠A to show that A is the vertex where the angle is measured.
• If a line (denoted by the dotted line in the diagram) connects Points B and C of the intersected Ray AB and Ray AC, then a right angle triangle is formed with the the points where the line BC intersects both rays serving as endpoints B and C of the triangle, now symbolized as △BAC. The △ is the symbol of the triangle. Because, ∠BAC is 90°, then it can written as ∟BAC, with the ∟ serving as the symbol of a right angle.
• If 3 rays originate from a common vertex, then 2 adjacent angles are created because the 2 angles share a common ray (or side).

• Consider 3 rays: Ray AB, Ray AC, and Ray AD. Ray AD intersects the angle formed by Ray AB and Ray AC to create two new angles from ∠BAC, with these angles being ∠BAD and ∠DAC. ∠BAD and ∠DAC are described as adjacent angles becuase they share a common side formed by Ray AD.
• Adjacent angles are subject to the angle addition postulate that states that the sum of adjacent angles is equal to the angle formed by the two rays on either end of the common side. Using this example, this postulate can be expressed as:

∠BAC = ∠BAD + ∠DAC.

• As can be noted, the Ray AD divides the △BAC triangle into 2 smaller triangles: △BAD and △DAC. If Ray AD bisects the line BC into two equal parts i.e BD = DC, then both △BAD and △DAC are right angle triangles with their right angles being ∟BDA and ∟ADC respectively.

Transversal and its Vertical, Opposing, and Corresponding Angles

• Two straight lines are different from each other if they do not share any of their endpoints. Any straight line that intersects these different straight lines is called a transversal.

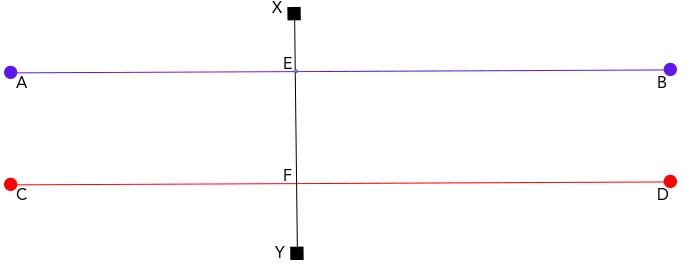
• At the point where the transversal intersects a straight line, four angles that add up to 360° are created. This is because the transversal bisects a straight line at a point to create a quadrant with two axes centered on that point. This quadrant can be represented as a circle that has 4 sections, each defined by its angle. These 4 angles can be described as the:
  • Upper Right Angle (URA) e.g ∠XEB and ∠XFD.
  • Lower Right Angle (LRA) e.g ∠YEB and ∠YFD.
  • Lower Left Angle (LLA) e.g ∠YEA and ∠YFC.
  • Upper Left Angle (ULA) e.g ∠XEA and ∠XFC.
• Vertical angles are angles that are opposite to each other on the same line, e.g the URA and the LLA are vertical angles. This means that ∠XEB and ∠YEA are vertical angles.

• Because the transversal intersects a minimum of 2 straight lines, then at least eight angles are formed – four angles on each line. Four of these eight angles are on one side (i.e right side) of the transversal, while the other four are on the other side (i.e left side).
• Any two angles – one on each straight line – formed on the same side of the transversal and on the same quadrant are called corresponding angles. For example, the 2 upper right angles – URA of Line AB and URA of Line B – are corresponding angles. Thus ∠XEB and ∠XFD are corresponding angles.
• The two angles formed on the same side of the transversal but facing each other are called internal opposing angles, or simply opposing angles. For example, the LRA of Line AB and the URA of Line CD are opposing angles, i.e ∠YEB and ∠XFD are opposing angles.
• The following postulates apply to angles formed by a transversal:
  1. The two angles formed on the same side of a transversal on the same straight line are supplementary pairs. For example, ∠XEB and ∠XEA are a supplementary pair. Other examples of supplementary pairs are ∠YEB and ∠YEA, ∠YFD and ∠YFC, ∠XFD and ∠XFC, and ∠YFD and ∠XFD.
  2. The vertical angles are equal to each other. For example, ∠YFD = ∠XFC, ∠YFC = ∠XFD, and ∠XEA = ∠YEB.

Two-Dimensional Euclidian Geometry

• The Elements of Geometry written by Euclid of Alexandria in circa 300 BCE (Before the Common Era) introduced the axiomatic system in geometry. This axiomatic system is made up of a set of consistent and non-contradictory axioms that can be used logically to derive a geometrical system. This geometrical system is called Axiomatic Geometry.
• An axiom is a fundamental geometrical principle or postulate. The angle addition postulate and the segment addition postulate are examples of axioms.
• The 5 Euclidian axioms can be reformulated as follows:
  • A straight line can be created using any two points.
  • A straight line can be extended into a straight ray.
  • Any point and its derivative line segment can be used as a radius to draw a circle.
  • Rights angles are always equal.
  • If a transversal crosses two straight lines, and the sum of two opposing angles on the same side of the transversal is less than a straight angle, then the two straight lines are not parallel lines and will intersect if extended enough. This axiom is called the parallel postulate and is the basis of Euclidian Geometries.
• The parallel postulate was later rephrased as Fairplay’s Axiom, which stated that “Given a line and a point not on the line, there is one and only one line that passed through the given point that is parallel to the given line.”
• In the example above, if ∠YEB + ∠XFD = 180°, then Line AB and Line CD are parallel lines. However, if ∠YEB + ∠XFD ≠ 180°, then Line AB and Line CD are not parallel lines.
• Euclidian geometries are any geometry that has at least a pair of parallel lines.

Plane Shape, Perimeter, and Area

• Perimeter and area are two of the main properties of a two-dimensional shape.
• A two-dimensional shape is also called a plane shape.
• Perimeter is the distance around a two-dimensional shape. This means that the perimeter can be calculated by simply adding the dimensions of all the sides of the shape.
• The simplest plane shape is the triangle, which has three sides and three internal angles (hence the designation tri-angle). A triangle can be considered as a shape formed when two intersecting lines are connected at their non-intersecting endpoints by a transversal that closes the triangle by creating its base.
• A rectangle can be considered as two parallel lines that have been intersected by two perpendicular transversals, hence creating four right angles inside the rect-angle, with any two pairs of these angles adding up to 180° (or straight [recta in Latin] angle).
• A rectangle whose length is equal to its width is called a square.

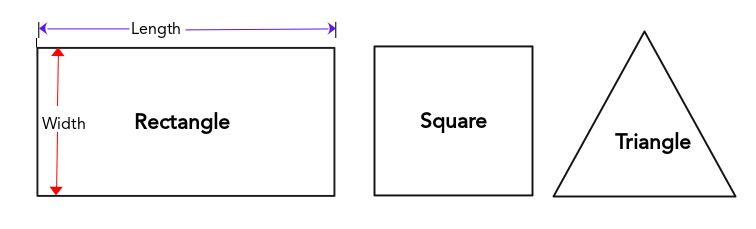
• The perimeter of a rectangle can be calculated easily as follows:

Perimeter = (2 × Length) + (2 × Width), which can be denoted simply as Perimeter = 2L + 2W.

• This is possible because the opposite sides in any rectangle have the same distance.
• For a square that has 4 equal sides, the perimeter can be calculated simply as:

Perimeter = (4 × Length) = 4L.

• The perimeter of a triangle is calculated by simply adding up the distances of all its three sides. Thus, in the triangle △BAC, the perimeter is calculated as:

Perimeter = BA + AC + BC

• Before calculating the perimeter or area of any plane shape, make sure that the units of measurement of all its sides are the same. For instance, the measurements of all sides must be stated only in inches or feet, but not in inches and feet, e.g the length is stated in feet but the width is stated in inches. This means that one must convert the measurements to only one unit of measurements.
• The amount of surface occupied by a plane shape is described as its area. This area is stated in terms of square units of measurements, e.g square feet or square inches. If one is using SI units, then the area is expressed as square meters or m².
• The area of a rectangle is computed by multiplying its length with its width, thus:

Area = Length × Width = LW

• For a square whose length and width are equal, the area is computed by simply squaring any of its sides, thus:

Area = Length × Length = L²

• A right-angled triangle is basically a rectangle bisected in half by a diagonal line intersecting at two opposite vertices. Thus, the formula for calculating the area of a triangle is:

Area = 1⁄2 × Length (Base of triangle) × Width (Height of triangle) = BH

• If a line is drawn through all the points that are equidistant from the center-point of a circle, then the line describes the perimeter of the circle, and the shortest distance between the center-point to any of the points in this line is called the radius of the circle. The radius is a straight line.
• The straight line that bisects the circle into two equal parts is the diameter of the circle. Because this diameter is simply two straight lines that originate at the center point of the circle, and then move in opposite directions at a straight angle so as to reach two opposite endpoints in the circle, then each line is a radius, and the diameter is the sum of two radii, or;

Diameter (D) = 2 × Radius = 2R.

• The perimeter of a circle is called its circumference, and it is calculated using this formula:

Circumference (C) = Pi (π) × Diameter = πD = π × 2R = 2πR

• The area of a circle is calculated using the formula:

Area = π × Radius² = π × (D/2)² = (π × D²)/4 = πR²

• Pi is basically the ratio of the circumference to the diameter of the circle, and its value is 3.142 (which is expressed fractionally as 22/7). Thus,

π = C:D = 3.142:1.

• The use of Pi allows for the area of a circle to be calculated from its known circumference if one does not want to first calculate the radius. This is done using the following formula:

Circumference²/(4π) = Area

The above formula also provides a way to calculate the circumference of a circle from its known area. This is done using the following formula:

Circumference = (2 × Area)/Radius

Problem 48 and the Egyptian Pi

• The ability to calculate the diameter from the area of a circle allows one to solve Problem 48 which was articulated in the Rhind Papyrus.
• Problem 48 is articulated as a statement that can best be rendered as follows: confirm that the area of a square whose side is 8 units is equal to the area of a circle whose diameter is 9 units. Thus, to confirm this statement, we use both formulas because the area and the diameter of the circle are known, and the calculation proceeds as follows:

Circumference = (2 × Area)/Radius, and Area of the Square = L² = 8 × 8.

Therefore, this equation can be solved as Circumference = (2 × 8 × 8) / (9/2) = (2 × 8 × 8 × 2)/9.

Now, the equation Circumference² / (4π) = Area can be rearranged to:

π= Circumference²/ (4 × Area), which computes to:

(2 × 8 × 8 × 2 × 2 × 8 × 8 × 2) / (9 × 9 × 4 × 8 × 8) = (2 × 8 × 8 × 2)/ (9 × 9) = 256/81 = 3.1605.

• Therefore, Problem 48 reveals the fact that Ancient Egyptians, or at least the author(s) of the Rhind Papyrus used a Pi whose value was 3.1605. This Pi value is sometimes called the Egyptian Pi, and it is quite impressive how close it is to the modern value of Pi.

Volume

• The amount of space occupied by a three-dimensional shape is known as its volume.
• Most formulas for calculating volume assume that one is dealing with a solid object.
• An object is any matter that has a three-dimensional shape. A better term to describe any three-dimensional solid shape is volumetric object.
• Volumetric objects are broadly classified into two categories: pyramid and prism.
• A prism is any three-dimensional shape with two identical bases, i.e the bottom base and top base. For example, a cylinder is a prism with a round bottom base and a round top base. A prism can have a triangular, rectangular, square, trapezoidal, pentagonal, hexagonal, heptagonal, or polygonal base. A prism with a square base whose height is equal to the length of this square is called a cube. Basically, all the dimensions in a cube are equal. A cuboid is a prism with a rectangular or trapezoidal base.
• The calculate the volume of a prism, one just needs to calculate the area of the base, and then multiply it by the height of the shape.

Volume = (Area of Base) × Height (H) of Object.

For the cube whose length is equal to its height, the Volume = L × L × L = L³.

• As expected, the units of measurement of all the sides of the prism must be the same before one starts to calculate the volume.

• Not every side of a prism can serve as its base as the following explanation shows. To begin with, the formula for calculating the volume assumes that the prism is standing on its base. For a rectangular or square prism, setting it to lie down still allows one to use the formula as the object still has two identical bases. However, if a triangular prism is made to lie down, then the top base and the bottom base are not identical.
• The formulas for calculating the volume of different types of prisms are derived below:

Rectangular Prism: Volume = (Area of Base) × Height of Object (H) = LW × H = LWH.

Square Prism: Volume = (Side[S] × Side[S]) × Height = S²H. A square prism whose height and side dimensions are the same is called a cube.

Triangular Prism: Volume = (½ × B × height[h] of triangle) × Height of Prism = ½ BhH.

Cylinder: Volume = πR² × Height of Prism = πR²H.

Polygonal Prism: Volume = (Area of Polygon) × Height of Prism

• Any volumetric object with only one base is called a pyramid. The shape of the base can be used to identify the type of pyramid as follows:
  • Cone – A pyramid whose base has a circular shape.
  • Triangular Pyramid – Any pyramid whose base is a triangle.
  • Square Pyramid – Any pyramid whose base is a square.
  • Polygonal Pyramid – Any pyramid whose base is a polygon.

• The volume of a pyramid is considered to be a third of the volume of a prism with an equivalent base and height. This simply means that the volume of a cone is a third of the volume of a cylinder whose base has the same radius as that found in the cone. To express it in a mathematical formulae:

Volume of a Pyramid = × (Volume of Prism with an equally sized base and height);

therefore, the volumes of the following pyramids can be calculated as:

Cone: Volume = 1/3 × (πR²H). = (πR²H)/3.

Triangular Pyramid: Volume = 1/3 × (BhH) = (BhH)/3.

Square Pyramid: Volume = 1/3 × (S²H) = (S²H)/3.

Polygonal Pyramid: Volume = 1/3 × (area of polygonal base) × Height of Pyramid

Making Weight a Component of Volume

• Calculation of volume has a practical application in material science, architecture, and construction where the size (or bulk) of objects must be considered alongside the object weight. In fact, volume can be related directly to the weight of an object using the following mathematical procedure. This weight is a factor of mass and density, and to calculate density, the following formula is used:

Density = Mass/Volume, which translates to Volume = Mass/Density.

Weight is calculated as: Weight = Mass × (Acceleration due to Gravity), and thus, Mass = Weight / (Acceleration due to Gravity).

Acceleration due to gravity, also known as gravitational acceleration, has a value of 9.764-9.834 meters per seconds squared (m/s²).

• The aforelisted formulas allow for the volume to be logically calculated using the following mathematical equation:

Volume = Weight/ {(Acceleration due to Gravity) × Density}.

Surface Area

• The two main geometrical properties of a three-dimensional object are its volume and its surface area.
• The surface area is the total amount of surface of a volumetric object, i.e the sum of the areas of all its sides.
• Equally, the surface area can be calculated for a plane shape, by simply multiplying its area by 2, i.e

Surface Area of a plane shape = Area × 2.

• For a volumetric object, each side of the three-dimensional shape is called a face, and therefore, the surface area of a square prism can be calculated as:

Surface Area = Area of Bottom Side (which can be denoted as Face₁) + Area of Top Side (Face₂) + Area of North Side (Face₃) + Area of South Side (Face₄) + Area of East Side (Face₅) + Area of West Side (Face₆). This can be summarized as:

Surface Area = Sum [denoted as ∑] of areas of (Face₁ + Face₂ + Face₃ + Face₄ + Face₅ + Face₆)

= ∑ (Face₁ + Face₂ + Face₃ + Face₄ + Face₅ + Face₆)

• The cube has faces that have the same length and width, and this means that the area of each face is equivalent to that of any other face. Therefore, the surface area of this cube/prism can be expressed as:

Surface Area of a Cube = ∑ (Face₁ + Face₂ + Face₃ + Face₄ + Face₅ + Face₆)

= (Area of any Face) × 6

= 6(Area of any Face)

• Apart from polygonal prisms whose faces have exactly the same dimensions, or a triangular pyramid made up of four equilateral triangles, other prisms and pyramids have dissimilar faces, and thus one must calculate the area of each face and then sum up all of these areas to get the surface area. This can be expressed mathematically as:

Surface Area = Area of Face₁ + Area of Face₂ + Area of Face₃ … (the ellipsis denotes more faces until the last face [denoted as Face_n] is reached) + Area of Face_n

• A cylinder is a special prism made up of a rectangle coiled around two circular faces, and thus its surface area can be calculated as follows:

Surface Area of Cylinder = Area of Rectangle + Area of Top Face + Area of Bottom Face

• Because the top and bottom faces have the same area, and the length of the rectangle is equal to the circumference of the circular base while the width of the rectangle is the height of the cylinder, then;

Surface Area of Cylinder = (2πRH) + (πR²) + (πR²) = 2(πR²) + (2∏RH); and using the principles of linear algebra, this equation can be reduced to:

Surface Area of Cylinder = πR (2H) + πR (2R) = 2πR (H) + 2πR (R)

= 2πR (H + R).

• An example of the application of surface area in real-world life is the amount of postal wrap one needs to cover a gift, or the amount of paint one needs to paint an object.

Similarity and Congruency

• Two objects that have exactly the same shapes, but are of different sizes, are called similar objects.
• Similar objects are used in modeling in engineering, where a model of the real object is created to be exactly like the object but scaled to be several magnitudes smaller in size. This means that the model is a fraction of the size of the real object, and this fraction is called the scaling ratio.
• The scaling ratio can be represented as SR, and the formula that relates the model to the real object is:

1/SR = Length of the real object/Length of the model object; therefore,

SR = (Length of the model object) / (Length of the real object).

• When comparing two triangles of different sizes, if all their corresponding angles are the same; then the triangles are similar. For example, angle ABC = ABC^’, Angle BAC=BAC’, and Angle ACB=ACB’ in the figure below. This property is known as congruency, and the angles are said to be congruent to each other. The mathematical symbol used to symbolize congruency is ≅.

• The congruent angles at their respective vertices are represented as follows:

∠B ≅ ∠B’, ∠A ≅ ∠A’, and ∠C ≅ ∠C’.

• Accordingly, this shows that triangle ABC is similar to triangle ABC’, and this is denoted as ABC ≅ A’B’C’.
• Because the angles are congruent, the sides of the two triangles are proportional to each other, and this is noted by the similarity of the triangles.
• The scaling ratio allows for the calculation of the area of any of two congruent shapes if the area of one of the similar shapes is known. The formula used is:

Area of Shape (of interest) = SR² × Known Area of a Similar Shape

• The above formula can be extended to apply to two similar volumetric objects, thus allowing for the calculation of the unknown volume of an object based on the known volume of a similar object.

Volume of Shape (of interest) = SR³ × Known Volume of a Similar Object

Pythagorean Theorem

• A triangle that has a right angle is called a right triangle.
• All angles inside the triangle add up to 180°.
• The triangle has three sides, and the longest side is called the hypotenuse. The hypotenuse is opposite the right angle which is formed by the intersection of two lines called the legs. Therefore, a triangle has three angles and three lines – two legs and a hypotenuse. The hypotenuse was initially described by philosophers as the line that subtends or stretches (in Greek, teinein) under (in Greek, hypo) the legs of a triangle. The two legs in the triangle are the Base Leg and the Height Leg.

• These three lines are related to each other mathematically through the Pythagorean Theorem which can be expressed as:

(Hypotenuse)² = (Base Leg)² + (Height Leg)².

• If one leg is longer than the other leg, then this leg is described as the length of the triangle, and the other leg is described as the width of the triangle. This relates the triangle to the rectangle by showing that a triangle is one of the two halves of a rectangle that has been bisected by the hypotenuse. Likewise, this transforms the expression of the Pythagorean theorem as:

(Hypotenuse)² = (Length)² + (Width)²

• The length and width of the triangle are usually referred to as the base and height of the triangle respectively, and this transforms the Pythagorean Theorem to:

(Hypotenuse)² = (Base)² + (Height)²

• An example of a right-angle triangle is the triangle whose legs measure 3 units and 4 units, and the hypotenuse is 5 units, and this 3-4-5 triangle was used in Ancient Egypt for land survey. Historians describe the 3:4:5 ratio of this triangle as the Pythagorean Triples. Ancient Egyptians did not have the concept of variables or the mathematical formula of the Pythagorean Theorem, and usually worked with whole numbers only. Thus, the rope used to survey the land had multiple knots, with each knot representing a whole figure of a specific distance. Therefore, the land surveyor would know that the land that measures 3 knots by 4 knots, had a diagonal distance of 5 knots.